Anyway, it put me in mind of an experiment I'd done a while ago to measure how long a capacitor could hold a charge. With a high quality capacitor it's difficult to do because a typical 10 M-ohm voltmeter will drain the voltage off in short order. So the trick is to connect the capacitor to the gate of a MOSFET, which has extremely high resistance, and charge the capacitor and put the voltmeter on the drain side of the MOSFET.
The effect on the drain circuit is hardly linear, but there's a sharp transition where the MOSFET comes out of saturation as the capacitor eventually charges toward zero volts. You can measure that transition gate voltage before hand and when the drain voltage rises to a certain reference point, you're there.
I was surprised at how long a certain film (I think) 0.22 uF capacitor held a charge. It had gone about four days when I accidentally discharged it, so even now I'm not sure. After that I tried an ordinary 0.1 uf ceramic disk and it held its charge for two days.
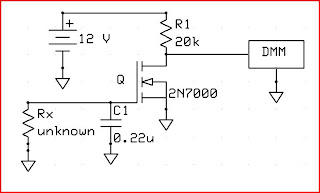
OK, so I know the self-discharge rate of the 0.22 uF capacitor was very slow, so I could use it to test large resistances and assume essentially all of the discharge was due to the external resistance. My circuit is simple enough to describe in words. A resistor, say 20k, from +12.7 VDC battery to the drain of the 2N7000 MOSFET. The source goes to ground. The gate goes to the capacitor and the other end of the capacitor goes to ground. The external resistance being "measured" goes from gate to ground, in parallel with the capacitor.
The MOSFET's channel is ON when the gate voltage goes positive and OFF when gate voltage is zero. So I measured that from a range of 10 V to about 2.25 V gate voltage, the MOSFET was fully on and drain voltage was near zero. Below 2.25 V gate voltage, the drain voltage started to rise and was at 8 V with 1.92 V on the gate and 12.5 V with 1.52 V on the gate. So when I see somewhere from 8 to 12 V on the drain, I know the capacitor has discharged to 1.5 to 2 VDC.
I set up a spreadsheet to figure resistance from V-initial, V-final, C and time 't', in seconds. Its uses the equation
R = -t / (C*ln(Vf / Vi))
Experiments
Turns out I don't actually have one of those anti-static pads but I do have some other stuff I wondered about. For one, those black foam rectangles you see ICs embedded in or affixed to, in the case of SMT. Another material is those shiny semi-transparent envelopes that the stuff we buy from Mouser or Digi-Key comes packed in.
I took a chunk of the black stuff, that used by AD to pack an AD9851 DDS chip in and stuck #18 solid wire electrodes in it lengthwise, about 1 inch apart and 1.5 inches deep and connected that across my capacitor. Connected the battery and then used a separate supply to charge the 0.22 uF capacitor to 10 VDC, at which time the drain voltage jumped from 12.5 VDC to 0 VDC. It took about 3 hours and 15 minutes for the voltage to start climbing and it quickly reached 11.8 VDC at 3 hours, 22 minutes. I inferred a gate voltage of ~1.85 volts from my earlier characterization of the 2N7000 and my spreadsheet spit out a value of 3.26E10 ohms, or 32.6 G-ohms between those electrodes.
Next I took one of those anti-static envelopes and inserted a couple pieces of circuit board material, about 1x2 inches as electrodes, spacing their long sides about 1/4 inch apart. So the conduction path is more or less across that 1/4 inch. I set a couple pieces of non-conductive "stuff" on top of the envelope to increase the contact area and started the timing thing again. This time it took 25 minutes & 22 seconds for the capacitor to discharge to the "threshold" region of about 1.9 V on the gate. The calculated resistance was 4.2E9 or 4.2 G-ohms. About one tenth of the reading with the black foam.
But it was interesting that I checked out a couple of other pieces of black spongy foam and measured resistances in the kilohms with my DMM, far too low to require my method.
My final experiment was a "control" test. The biggest resistor I have is marked 66 M-ohms at 10% tolerance. I connected it to the gizmo and saw the drain voltage quickly transition at 24 seconds. Spreadsheet says, 67.8 M-ohms. So I think the accuracy is pretty good.
In the interest of scientific rigor, I should say that I just arbitrarily measured the resistance between two points, or two electrodes. If I were being rigorous, I would have made things more complicated and attempted to measure volume or surface resistivity of the material. But my intent was just to answer the question, "I wonder what the resistance is between these two electrodes in or on this anti-static material?"
BTW, the 0.22 uF capacitor was just what I pulled out of the box. To keep the times from being excessively long, a capacitor an order of magnitude or so smaller would be a good idea, after verifying that its self discharge rate is appropriately long.
Nick, WA5BDU
3/27/2010
Here's an edit. It was suggested that a schematic would be a good idea, however simple this thing may be. I guess that's true:
So there's one. I charged C1 to 10 V to start the measurement, but there's no reason you couldn't just touch the battery positive to it to charge it. As long as you know the initial and final voltages, you're good. Another option would be to charge C1 to a value of the final target "threshold" voltage divided by 0.37. Since a capacitor will discharge to 37% of its initial voltage in one time constant, it simplifies the math of finding Rx. Like this -
tau = RC (tau is one time constant)
so, R = tau / C
3/28/2010
No comments:
Post a Comment